Câu 1. Hình chữ nhật bốn màu (6 điểm).                                  
Trên mặt phẳng tọa độ Đề các vuông góc Oxy cho n điểm phân biệt Ai(xi, yi) với i = 1, 2, 3, …, N.   Mỗi điểm Ai được tô bởi màu Ci thuộc {1, 2, 3, 4}. Ta gọi hình chữ nhật bốn màu là hình chữ nhật thỏa mãn hai điều kiện sau:
   Bốn đỉnh của hình chữ nhật là bốn điểm trong N điểm đã cho và được tô bởi bốn màu khác nhau.
   Các cạnh của hình chữ nhật song song với một trong hai trục tọa độ.
Yêu cầu: Cho biết tọa độ và màu của N điểm, hãy đếm số lượng hình chữ nhật bốn màu.
Dữ liệu vào: Cho trong file văn bản có tên COLOREC.INP có cấu trúc:
   Dòng 1: Chứa số nguyên dương N là số lượng điểm trên mặt phẳng (4 ≤ N ≤ 105).
   Dòng thứ i trong n dòng tiếp theo chứa ba số nguyên xi, yi, ci là thông tin về tọa độ và màu của điểm thứ i (i = 1, 2, 3, .., N), (|xi|, |yi| ≤ 200).
(Hai số liên tiếp trên cùng một dòng được ghi cách nhau ít nhất một dấu cách)
Dữ liệu ra: Ghi vào file văn bản có tên COLOREC.OUT với cấu trúc:
   Dòng 1: Ghi một số nguyên là số lượng hình chữ nhật đếm được.
Ví dụ:
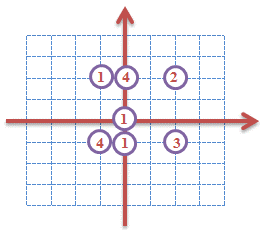
COLOREC.INP 
7
0 0 1
0 1 4
2 1 2
2 -1 3
0 -1 1
-1 -1 4
-1 1 1
COLOREC.OUT
2

 ![](/media/martor/93373228-741c-4336-9989-10f35bc62489.png)

* Giới hạn: 50% số test ứng với 50% số điểm của bài có 4 ≤ n ≤ 100

Câu 2. Đường đến trường (7 điểm).
Ngày 20/9/2022 Sở GD&ĐT Quảng Bình tổ chức kỳ thi chọn đội tuyển chính thức dự thi học sinh giỏi Quốc gia tại điểm thi trường THPT Chuyên Võ Nguyên Giáp. Tất cả các bạn đã chuẩn bị khá kỹ càng. Chỉ có điều, các thí sinh dự thi rất lo lắng cho Nam vì nhà Nam cách điểm thi khá xa và bạn ấy không xác định được đi đường nào đến điểm thi là nhanh nhất. Thường ngày mọi người không quan tâm đến điều này, nhưng hôm nay là kỳ thi rất quan trọng nên không muốn bạn Nam đến trễ.     
Bản đồ thành phố Đồng Hới gồm có N nút giao thông và M con đường nối các nút giao thông này. Có 2 loại con đường là đường 1 chiều và đường 2 chiều. Độ dài của mỗi con đường là một số nguyên dương. Nhà Nam ở nút giao thông 1, điểm thi Trường THPT Chuyên Võ Nguyên Giáp ở nút giao thông N. Vì một lộ trình đường đi từ nhà Nam tới điểm thi có thể gặp nhiều yếu tố khác như là gặp nhiều đèn đỏ, đi qua công trường xây dựng, ... phải giảm tốc độ cho nên Nam muốn biết là có tất cả bao nhiêu đường đi ngắn nhất đi từ nhà tới điểm thi. Các bạn thí sinh hãy lập trình giúp Nam giải quyết bài toán này.
Dữ liệu vào: Cho trong file văn bản có tên SCHOOL.INP có cấu trúc:
   Dòng 1: Chứa hai số nguyên N và M (1 ≤ N ≤ 5000; 1 ≤ M ≤ 20000).
   M dòng tiếp theo, mỗi dòng ghi 4 số nguyên dương K, U, V, L. Trong đó:
+ K = 1 có nghĩa là có đường đi một chiều từ U đến V với độ dài L.
+ K = 2 có nghĩa là có đường đi hai chiều giữa U và V với độ dài L.
(1 ≤ U,V ≤  N; L ≤ 32000)
(Hai số liên tiếp trên cùng một dòng được ghi cách nhau bởi ít nhất một dấu cách)
Dữ liệu ra: Ghi vào file văn bản có tên SCHOOL.OUT với cấu trúc:
   Dòng 1: Ghi 1 số là độ dài đường đi ngắn nhất.
   Dòng 2: Ghi 1 số là số lượng đường đi ngắn nhất. 
Biết rằng số lượng đường đi ngắn nhất không vượt quá phạm vi int64 trong pascal hay long long trong C++.
Ví dụ:
SCHOOL.INP  
3   2 
1   1   2   3
2   2   3   1
SCHOOL.OUT
4
1

Câu 3. Xếp hàng (7 điểm).
Để trình diễn một tiết mục trong màn khai mạc Đại hội thể thao quốc tế, đạo diễn Hùng đã mời n vận động viên có chiều cao khác nhau từng đôi một tham gia. Theo kịch bản, n vận động viên sẽ được xếp thành một hàng dọc, đầu hàng ở phía khán đài A (khán đài chứa các khách mời quốc tế), cuối hàng ở phía khán đài B (khán đài có nhiều du khách và các quan chức địa phương). Đạo diễn muốn rằng từ phía khán đài A, khán giả có thể nhìn thấy P vận động viên, còn từ phía khán đài B khán giả có thể nhìn thấy Q vận động viên. Một vận động viên được nhìn thấy từ phía khán đài A nếu như tất cả các vận động viên đứng trước (theo chiều từ đầu hàng đến cuối hàng) đều có chiều cao thấp hơn vận động viên này. Một vận động viên được nhìn thấy từ phía khán đài B nếu như tất cả các vận động viên đứng sau (theo chiều từ đầu hàng đến cuối hàng) đều có chiều cao thấp hơn vận động viên này.
Ví dụ: Có 9 vận động viên được xếp theo thứ tự với dãy chiều cao tương ứng là 
3, 2, 4, 1, 9, 8, 7, 5, 6
thì từ khán đài A (ở phía bên trái) có thể nhìn thấy 3 người (với chiều cao là 3, 4, 9), còn từ khán đài B (ở phía bên phải) có thể nhìn thấy 4 người (với chiều cao là 6, 7, 8, 9). 
Yêu cầu: Hãy giúp đạo diễn xác định xem có bao nhiêu cách xếp n vận động viên thành hàng dọc thoả mãn điều kiện đặt ra. 
Dữ liệu vào: Cho trong file văn bản có tên QUEUE.INP có cấu trúc:
   Dòng đầu tiên ghi ba số nguyên dương n, P, Q (n  2000; P, Q  n).
   Dòng thứ hai gồm n số nguyên dương là các độ cao của n vận động viên được mời tham gia thực hiện tiết mục trình diễn. 
(Hai số liên tiếp trên cùng một dòng được ghi cách nhau bởi ít nhất một dấu cách)
Dữ liệu ra: Ghi vào file văn bản có tên QUEUE.OUT với cấu trúc: 
   Dòng 1: Gồm một số nguyên là phần dư trong phép chia số lượng cách xếp tìm được cho 109+7.
Ví dụ:
QUEUE.INP   
3   2   1
1   2   3
QUEUE.OUT
1
Giải thích: Trong số 6 cách xếp 3 vận động viên thành một hàng dọc, có một cách duy nhất các vận động viên được xếp theo thứ tự chiều cao là 2, 1, 3 thoả mãn yêu cầu đặt ra: Nhìn từ khán đài A thấy được 2 vận động viên 2,3; nhìn từ khán đài B thấy được 1 vận động viên 3
* Giới hạn
𝑛 ≤ 10: 30% số điểm
𝑛 ≤ 500; 𝑄 = 1: 30% số điểm
𝑛 ≤ 500: 20% số điểm
𝑛 ≤ 2000: 20% số điểm 
-------------hÕt------------